Kathleen Ollerenshaw
Lattice Points in a Circular Quadrilateral Bounded by the Arcs of Four Circles
Quarterly Journal of Mathematics, Oxford Series 17, (1946) 93-98
[Received 1 May 1945]
Introduction
Recently Mordell has proved some general theorems concerning lattice points in non-convex regions. In particular he has considered a circular quadrilateral bounded by arcs of equal circles which form a region resembling an asteroid. In this note I find similar results for another closed, non-convex circular quadrilateral E, which is shown in the figure and presently defined. The proof of these results provides an extremely simple example of Mordell's method: probably as simple as any that can be found.
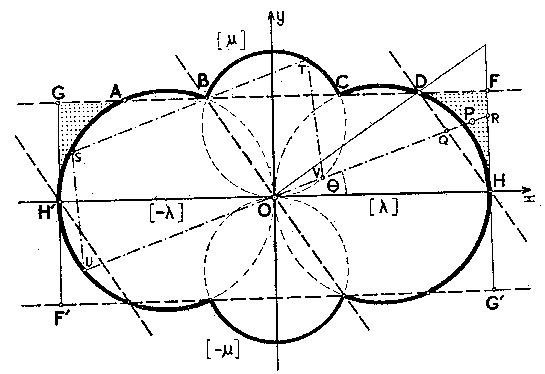
[Definition of critical lattice omitted]
The region E is bounded by the arcs of four circles [±λ], [±μ], defined by the equations
x2 + y2 = ±λx, x2 + y2 = ±μy.
More precisely, if P is any point of E, then its coordinates (x,y) must satisfy the inequality
min{|(x2 + y2)/λx|, |(x2 + y2)/μy|} < 1, (4)
where λ, μ are positive numbers. The transformation x —> y, y —> x merely interchanges λ, μ in (4). There is therefore no loss of generality in taking λ > μ. In the convenient terminology of figure-skating, the four defining circles form two "eights" with common centre and perpendicular axes: in fact, the particular domain arose out of demonstration of figure-skating on the frozen static-water tank of an Oxford college.
