Mary E. Sinclair
Concerning a Compound Discontinuous Solution in the Problem of the Surface of Revolution of Minimum Area
The Annals of Mathematics, 2nd Ser., Vol. 10, No. 2 (Jan. 1909), 55-80
Introduction
Among the minimum surfaces which can be represented by liquid films is a surface of revolution across which is a transverse plane circular film. It can be constructed by placing one on the other two equal rings, dipping them into soap solution, and then drawing them apart always parallel to each other and perpendicular to an axis through their centers. A longitudinal section of the surface shows on each side of this axis a system of three curves meeting in a point, two of the curves extending respectively to the two rings, and the third extending to the axis. The experiment suggest the following mathematical problem:
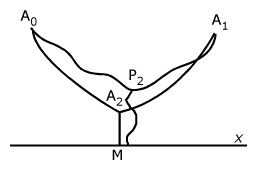 Given two points A0 and A1 in the xy-plane and on the same side of the x-axis. Join the points by a curve confined to the positive side of the x-axis, and from an arbitrary point P2 of this curve draw a curve to the x-axis. To find among all such systems of curves that one which when revolved about the x-axis shall determine a surface of revolution of minimum area. All curves which we consider will be of class D1.
Given two points A0 and A1 in the xy-plane and on the same side of the x-axis. Join the points by a curve confined to the positive side of the x-axis, and from an arbitrary point P2 of this curve draw a curve to the x-axis. To find among all such systems of curves that one which when revolved about the x-axis shall determine a surface of revolution of minimum area. All curves which we consider will be of class D1.
Footnote: A curve is of class D1 if it is continuous and consists of a finite number of arcs each of which has a continuously turning tangent.
The object of the present paper is to give a solution of this problem. The discussion is divided into three parts A, B, C, dealing, respectively, with the necessary conditions for the solution, the sufficient conditions, and the character of the field of extremals. The principal results obtained are as follows:
- The solution must consist of two catenaries A0A2, A2A1, with the x-axis for directrix, and the normal A2M from A2 to the x-axis. The catenaries must meet the normal A2M under an angle of 120°.
- On the arc A0A2 there exists a critical point A0*, a limit on the left for the position of A0; on the arc A2A1 there exists a conjugate point A0', a limit on the right for the position of A1. For the latter point there exists a simple geometric construction which we shall call the Lindelöf construction for our problem.
- The above are not only necessary but also sufficient conditions for a relative minimum.
- The solution is unique within a field defined by the one-parameter set of extremal-systems passing through A0, defined in 1 above.
- The field consists of two parts in which the area of the surface of revolution given by our solution is respectively greater or smaller than that given by the solution found by Goldschmidt [Prize Essay, 1830].
- Experiment verifies the results defining the position of the conjugate point.
Full article available from JSTOR.
