B. M. Turner
On the Positions of the Imaginary Points of Inflexion and Critic Centers of a Real Cubic
The Annals of Mathematics, 2nd Ser., Vol. 23, No. 4 (June 1922), 287-291
Introduction
In the extensive study of the configuration formed by the points of inflexion of a real cubic, it appears that no one has considered the possible positions of the six imaginary points of the group when the real three points are fixed. This is worthy of consideration for these two sets of points are so related that, while the three collinear real points of inflexion impose only five conditions and hence determine a fourfold infinite system of cubics in a plane, not one of the six points can be chosen arbitrarily. The following gives a construction for such a set of six points when the three real points are taken arbitrarily on a line; and by a generalization accounts for all such possible sets of six points.
The construction for the six imaginary points of inflexion also serves to show the positions of the twelve critical centers for the non-singular real cubic.
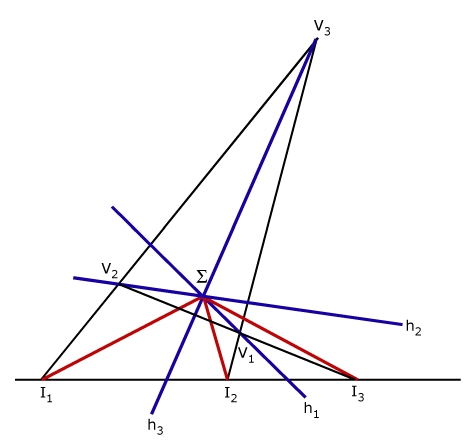
Construction
Let any three real points I1, I2, I3 on an arbitrary real line be taken as points of inflexion for a real cubic. Let Σ be any other real point. Join Σ to the points Ii and construct the fourth harmonic to each one of these lines with respect to the other two. Denote the fourth harmonic to the line through I1 by h1 and similarly for I2 and I3. Through any one of the three points, say I1, draw an arbitrary real line intersecting h2 and h3 in V2 and V3. Draw the lines I2V3, I3V2 intersecting in V1 on h1. The projections upon the sides of the triangle V1, V2, V3 through Σ, of the two points equianharmonic to the three points I, are six imaginary points which together with Ii form an inflexional group for a real cubic.
