Dame Kathleen Ollerenshaw and Sir Hermann Bondi, F.R.S.
Magic Squares of Order Four
Philosophical Transactions of the Royal Society of London, Vol. 306 (October 15, 1982), 443-532
Excerpt
 |
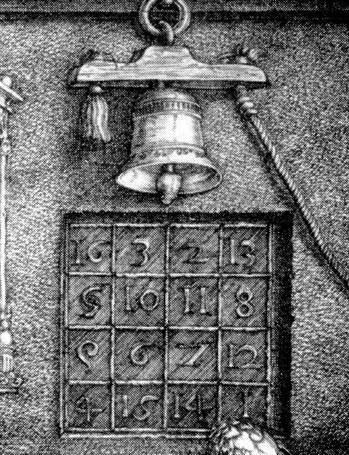 |
| Albrecht Dürer's Melancholia | 4x4 magic square, upper right corner |
A magic square is said to be symmetrical if each of those pair of numbers which are symmetrical in the centre point of the square add to half the sum of the numbers in each row, column, and principal diagonal – here 17. The magic square shown above, seen in the famous engraving entitle Melancholia by Albrecht Dürer (1471-1582) is symmetrical...The square contains the deliberate pun of the date of the engraving, 1514, appearing at the centre of the bottom row. From the list of solutions in this paper it is easily checked that there are 32 essentially different magic squares which can be written with the numbers 15, 14 in these positions, but only four of them, of which Dürer's is one, are symmetrical.
| 16 | 3 | 2 | 13 |
| 5 | 10 | 11 | 8 |
| 9 | 6 | 7 | 12 |
| 4 | 15 | 14 | 1 |
